Why emissivity matters
First of all let us simplify a couple of terms, which might otherwise cause confusion. There is albedo, reflectivity, absorptivity and emissivity. In climate science they somehow all mean the same thing. Albedo literally means the same thing as reflectivity, it really makes no difference. Then according to Kirchhoff's law absorptivity = emissivity at any respective wavelength. And since transmissivity is usually and rightfully ignored in this discipline, both absorptivity and emissivity respectively are just the inversion of albedo or reflectivity. So absorptivity = emissivity = 1 - albedo = 1 - reflectivity.
We only even distinguish between absorptivity and emissivity and the way that absorptivity is usually considered with SW radiation, and emissivity with LW radiation. The distinction is relevant as the one intrinsic variable (whatever term you want to use for it), differs with wavelength. For standardization I prefer to call it reflectivity.
As I have pointed out already in climate science the term albedo is used a lot, meaning SW reflectivity. At the same time it is constantly suggested Earth was emitting like a blackbody, implicitly denying LW reflectivity. And for some odd reason it seems to work. The minds get so confused by constant repetition of non sense, that apparently the most basic intelligence functions fail. If you have my somewhat cynical view on people's intellect, which is mainly an imitation game, then it is not much of a surprise. People hold true and "logical" what they hear most often, a controlling autonomous self-stabilizing filter is largely lacking.
Anyhow, let us look at the reflectivity of water in the range of 0.2 to 100µm, which is covering both the SW and the LW range. I have plotted it against the planck curves for solar SW radiation and terrestrial LW radiation, dimensionless just to give an idea on the weighting. As we can see reflectivity undergoes distinct variations over different wavelengths. And it turns out (spoiler alert!) that reflectivity is larger in the LW range than in the SW range.
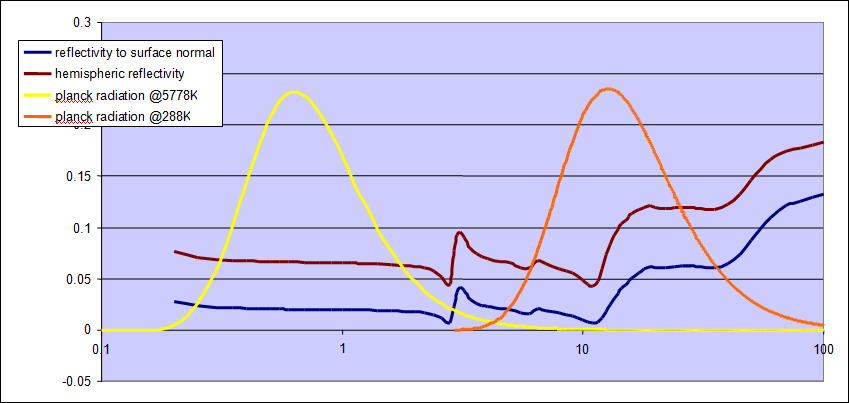
I think the example illustrates very well what a fundamental blunder it is, to only consider SW reflectivity while assuming there was none in the LW range. Just in case you do not know LW reflectivity, it is the best and most reasonable approximation, the golden rule so to say, to assume it was identical to that in the SW range. So the quotient of absorptivity / emissivity, which you need to calculate the theoretic temperature of any surface, should always be set to 1 by default. That is unless you have accurate information on BOTH terms. Never ever you may include a realistic parameter for absorptivity while holding emissivity = 1, just because you do not know it. That would be totally idiotic!
So how is the GHE of Earth calculated again? Right, by including SW reflectivity (aka albedo = 0.3) and assuming there was no LW reflectivity. There is one basic rule to avoid the most fundamental beginner's mistake. And how does super sophisticated, "settled" climate science deal with it, right at it's foundation? It jumps right in! Really, you can not make this up.
((1-0.3)/1 * 342 / 5.67e-8)^0.25 = 255K
I am dealing with the mess this causes throughout the site, but here I would like to point out a specific view, since it will open up some interesting perspectives. With this basic approach we can not just calculate the theoretic temperature of Earth, but also that of other celestial bodies, most notably the moon.
The surface temperature of the moon causes a lot of confusion, since there is a huge spread between day and night side. Over 99% of the radiation emitted is from the hot day side and almost none by comparison from the night side. Radiation is a function of temperature by the power of 4. Doubling the temperature means 16times as much radiation. Equally if you have two surfaces, one 16times smaller but twice has hot as the other, they will emit the same amount of radiation.
For the moon that means the hot day side consumes most solar irradiance as it emits plenty of LWIR right back into space and only little heat will be stored for the night. An arithmetic mean of surface temperature thus will be relatively low (~210K), but it does not mean a lot. It seems more reasonable to average by the power of 4, which should give some 276K, corresponding to the average emission temperature.
To simplify things and avoid a lengthy discussion, we can focus on maximum temperatures only. With the sun in the zenith the surface will receive the full, undiluted solar irradiance of some 1368W/m2. If we assume an albedo of 0.12 we can accordingly calculate what maximum temperature the moon could get at the equator.
((1-0.12)/1 * 1368 / 5.67e-8)^0.25 = 381.7K
The actual average maximum temperature however is rather 394K123. "Maximum average" may sound a bit strange, the reason is actual maximum temperatures can exceed 400K in some craters, where the ridges provide some additional radiation (reflected and emitted) towards the center. But with a flat surface it is about 394K, as the Diviner4 lunar temperature map below shows.
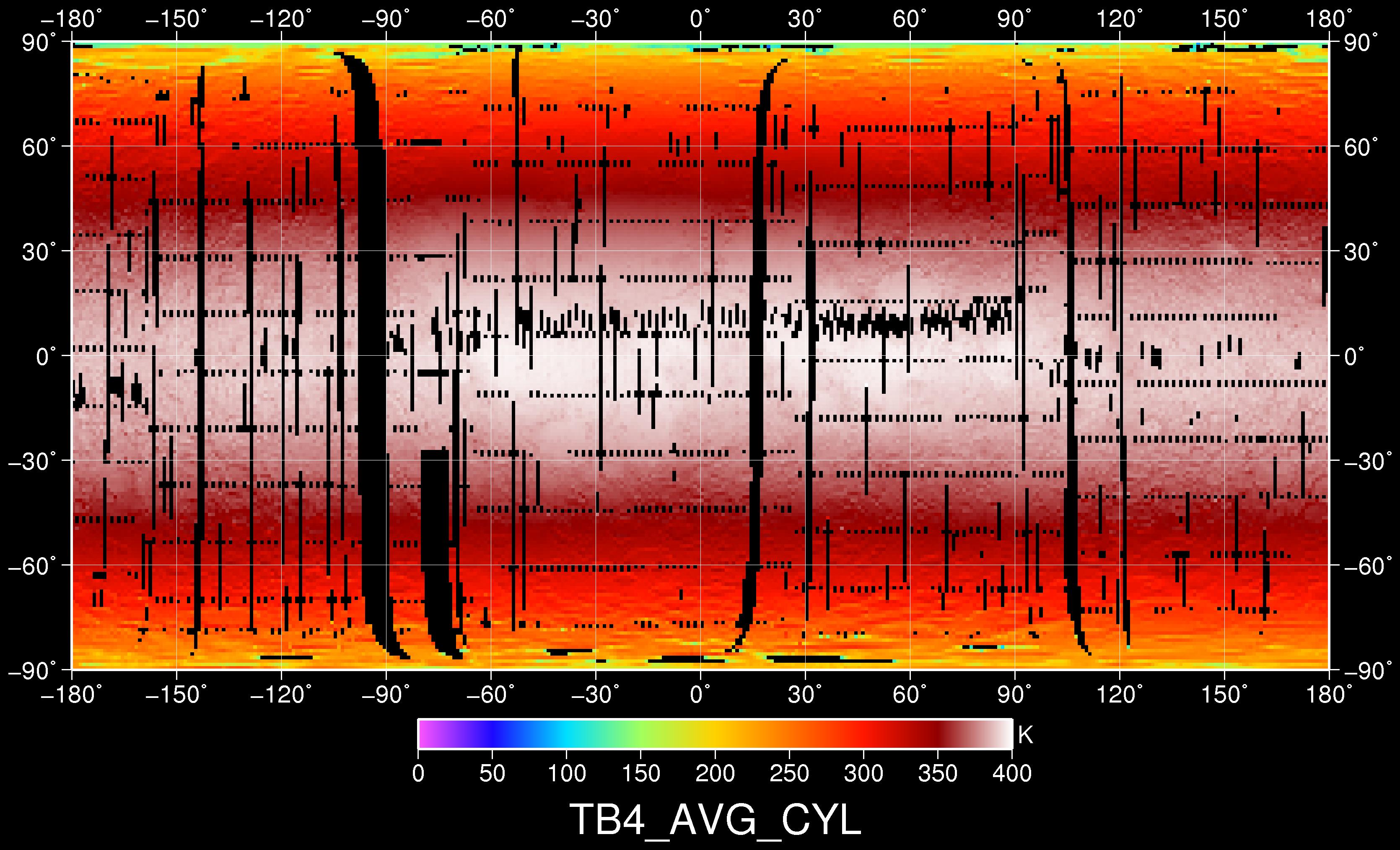
So we got a little bit of a problem here. The same formula that tells us Earth had a GHE of 33K, is telling us the moon had a GHE of ~12K, at least in this specific instance. Now we know the moon has no atmosphere and there can not possibly be a GHE. The reason for that contradiction is pretty obvious, also since we have discussed it already. We did not account for LW reflectivity, or LW albedo if you will. Doing so will always give you a calculated theoretical temperature which is too low and compared to observed temperature, you get an erroneous "GHE".
With given insolation and albedo, there is only one value for LW reflectivity that will give us 394K, and that is 0.12, or 0.88 for emissivity respectively. Since 0.88/0.88 = 1 the moon takes on the same temperature as a perfect black body. The golden rule applies and absorptivity and emissivity cancel each other out. Something NASA is certainly aware of, except for their "climate department" maybe.
Yet there is a funny twist to it. A satellite like the LRO (lunar reconnaissance orbiter) measures radiation and if you know emissivity, it is easy to tell what temperature there is. And if you know the temperature, you could easily tell emissivity. But if you know neither emissivity nor temperture, the measured radiation is insufficient information. Even if you stood on the moon, it would be extremely hard to accurately measure surface temperature. If you stick a thermometer into the soil, the part that reaches out will be heated by the sun itself, but that is not what you are after. Then the surface is a very thin layer of regolith with low conductivity. So, how does it work at all?
The answer is simple. The emissivity of 0.88 is more of an educated guess, not a solidly measured value. Yes, there may be some hints with the planck curve, but that is not so precise either. It means not just the data here do support the golden rule, but NASA is actively assuming it, for all the reasons I named, and maybe more. But only when it comes to climate science, this rule and many others mysteriously shall not apply.



Comments (2)
David Loucks
at 29.06.2022https://phzoe.com/2019/11/05/what-is-earths-surface-emissivity/
David Loucks
at 29.06.2022https://phzoe.com/2022/06/11/shrinking-the-atmospheric-greenhouse-effect-closer-to-reality/