Ok, this is a purely theoretical article and probably it could not get any more boring than this. Also it should be totally unnecessary to even explain such a basic logic. One could make it a simple question within an IQ test, so at least the article will be short. Yet on the other side there are two reasons making it totally necessary to explain. First of all, most people fail on some IQ test questions, which is the reason why not everyone has at least some 145 IQ, a minimum requirement to do science I would say. Also having many unqualified scientists will not be compensated by “consensuses”, rather it will only make matters worse. Secondly “climate science” fails on this account in every thinkable way, by intent or not, next to a lot of laymen stumbling here, which a lot of blogs testify. We just can not have that any longer, not if the fix is so cheap.

I have skilfully drawn two geometric figures. We have a rectangle (R) 3x6cm in size and a circle (C) with a diameter of 4cm, half overlapped with the rectangle. The area covered by the R is 18cm2, that of the C is 2x2xPI = 12.57cm2. The area covered by both R and C is 18 + 12.57/2 = 24.28cm2, less than the sum of R and C as the overlap will not count twice.

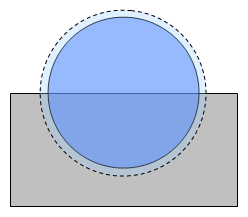
The “complicated” question now is, what happens if C should grow by 10% in diameter? How much more area will be covered by both geometric figures? We can easily find C is going to grow by (1.1^2-1)*12.57 = 2.64cm2. However half of that growth will be overlapped with R, so that it will not increase the combined area at all. Rather the combined area will only grow by 1.32cm2 to 25.6cm2.

Simple as it is, there are a couple of important lessons to be learned here. Half of the area of C is covered by both, C and R. Removing either C or R will not make it “uncovered”. Equally C only adds half of its area to the combined area. Most importantly if C should grow it will add only half of that growth to the total, combined coverage, at least if this growth is symmetric. Not incidentally this ratio (50% in our example) will be true both for the given addition by C, as to any delta should C change its size. Also we should see the other half of growth simply expands the overlap, which in terms of total area covered is irrelevant. From this we may conclude the NET(!) coverage by C will be the proper basis to derive any delta in total coverage, should C grow or shrink.

Will this always be true? No! Given the geometry here, if R should grow proportionate in all directions, the overlap will grow to a lesser percentage as the net coverage by R. With another geometry the opposite could be true. It is something to bear mind. Either way, the net coverage by C or R will serve as a better approximation to predict total coverage, should any of its agents change in size, than gross coverage.

The danger is, that if do not pay attention to these overlaps and you take gross coverage as a basis, you might falsely add the additional overlap to the overall area. Then if there are more agents, like R, growing as well, as feedbacks for instance, you might count the overlaps multiple times, despite you must not even count them once. In this way the margin of error will not just add up, but rather multiply.

On top of that add the original sin, which is ignoring the overlaps with clouds and real life surface emissivity, both necessary to assess the net coverage, and you get a hyperinflation of error margins, all pointing in the same direction. In fact, as we are going to see, an incredible 80-90% of ECS are made up by these errors. It originates in the concept of looking at the different agents one by one, within a theoretical framework that is far off reality and then linearly extrapolating it.

It is a bit reminiscent of “the germ is nothing, the terrain is everything” (Pasteur considering an alternative view). Arguably the germ is not nothing, regrettably, but certainly the “terrain” is to be considered. And in climate science a single agent like CO2 can not be understood without the environment it is embedded in. And despite every single “climate scientist” would indignantly deny such an accusation, the truth is they never paid attention. No one!